Voici un exemple de calcul de l’intervalle de confiance autour d’un score observé à un instrument psychométrique.

Lors d’un processus de sélection, Sylvie a obtenu un score de 121 à l’échelle d’aptitude verbale de la Batterie Générale de Tests d’Aptitudes (BGTA), dont l’ÉT est de 20 et le coefficient de fidélité (r) est de 0,91. Quel est le degré de précision réel de cette échelle de la BGTA? En d’autres mots, à quel point le résultat obtenu par Sylvie est-il précis? Pour les besoins de l’exercice, calculons l’intervalle de confiance pour deux seuils de probabilité, soient 68 % et 95 %.

Nous devons d’abord calculer l’erreur-type de mesure, selon la formule suivante et avec les données fournies au paragraphe ci-dessus.

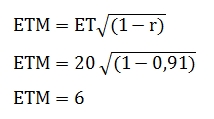L’erreur-type de mesure de cette échelle est donc de 6 points. On dira alors que la marge d’erreur à 68 % de l’échelle d’aptitudes verbales de la BGTA est de plus ou moins 6 points, ou encore, qu’il y a 68 % de probabilité que le score vrai de Sylvie se trouve à plus ou mois 6 points du score observé.  Pour obtenir l’intervalle de confiance à 68 %, il faut ajouter l’ETM au score de Sylvie :

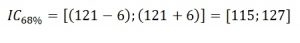On dira alors que le score vrai de Sylvie à l’échelle d’aptitude verbale de la BGTA a 68 % de probabilité de se trouver à l’intérieur de l’intervalle de confiance calculé, soit entre 115 et 127. Il y a donc 32 % de probabilité que le score vrai de Sylvie soit en vérité inférieur à 115 ou supérieur à 127.

Afin d’avoir un degré de certitude plus élevé , l’ETM peut être calculé avec un seuil de confiance à 95 % :

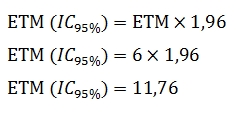Ainsi, la marge d’erreur à 95 % sera de plus ou moins 12 points. L’intervalle de confiance à 95 % doit alors être calculé ainsi :

On dira alors que le score vrai de Sylvie a 95 % de probabilité de se situer entre 109 et 133.

Ces calculs illustrent bien que plus le seuil de probabilité choisi est élevé, plus la marge d’erreur est grande et plus l’intervalle de confiance est grand.

Si le point de coupure entre les candidats retenus et les candidats non-retenus lors de ce processus de sélection avait été de 124 à l’échelle d’aptitude verbale de la BGTA,  la candidature de Sylvie, en se basant uniquement sur son score de 121, n’aurait pu être refusée, puisque  son score vrai a 68 % de probabilité de se trouver entre 115 et 127, et 95 % de probabilité de se trouver entre 109 et 133. Il est donc possible qu’elle ait en vérité le niveau d’aptitude requis (il est probable que son score vrai soit égal ou supérieur à 124).

Cet exemple illustre l’importance de tenir compte de l’erreur de mesure et de l’intervalle de confiance dans l’interprétation des résultats à un instrument psychométrique.