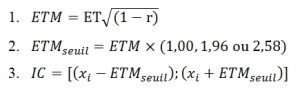En s’appuyant sur la distribution théorique des scores observés, l’intervalle de confiance (IC) détermine les balises (les bornes) de part et d’autre du score observé, à l’intérieur desquelles le score vrai de l’individu a une probabilité de se trouver. L’intervalle de confiance est très important pour l’interprétation des résultats d’un instrument psychométrique. Il représente en fait la marge d’erreur de la mesure, selon laquelle nous devons relativiser l’interprétation du score observé. Lorsqu’un instrument a une fidélité élevée, l’erreur de mesure est faible, donc l’intervalle de confiance est petit et la confiance que l’on peut accorder aux résultats s’en trouve renforcée. À l’inverse, un outil psychométrique dont l’erreur de mesure est élevée a un large intervalle de confiance et la confiance que l’on peut avoir dans ses résultats est plus faible.
Les limites (les bornes) de l’IC sont toujours déterminées en fonction de l’erreur-type de mesure (ETM) et d’un seuil de probabilité. L’étendue relative au seuil de confiance recherché (souvent 90 % ou 95 %) est fournie par les tables de fréquences des valeurs de la distribution normale. À cet effet, rappelons que dans une distribution normale, 95 % des observations se situent à l’intérieur de l’étendue de -1,96 écart-type (ÉT) et +1,96 ÉT, et que 99 % des observations se situent à l’intérieur de l’étendue de -2,58 ÉT et +2,58 ÉT.
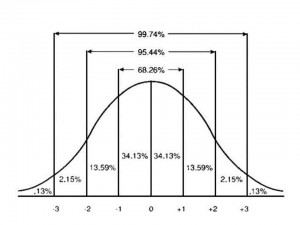
Rappelons aussi que l’ETM est en fait l’ÉT de la distribution théorique des scores observés d’une même personne à la passation d’un instrument psychométrique. Puisque le score vrai correspond à la moyenne de la distribution théorique des scores observés, il y a alors 95 % de probabilité que le score observé se situe entre -1,96 ETM et +1,96 ETM du score vrai. Comme on connaît le score observé mais pas le score vrai, on ne peut calculer cet intervalle de confiance autour du score vrai. Cependant, en déplaçant l’IC autour du score observé, on dira que l’IC indique la probabilité que le score vrai se situe à l’intérieur de l’IC autour du score observé. On dira donc que nous sommes certains à :
- 68 % que le score vrai se situe entre -1 ÉTM et +1 ÉTM du score observé;
- 95 % que le score vrai se situe entre -1,96 ÉTM et +1,96 ÉTM du score observé;
- 99 % que le score vrai se situe entre -2,58 ÉTM et +2,58 ÉTM du score observé.
Le calcul de l’intervalle de confiance autour d’un score observé se fait donc à partir de l’ETM ainsi que du degré de confiance que nous souhaitons avoir en cette erreur de mesure.
La formule suivante permet de calculer l’intervalle de confiance.
où xi = score observé à l’instrument psychométrique
Ainsi, pour connaître l’intervalle de confiance dans lequel un score vrai a une probabilité de se trouver, la démarche complète est la consiste à :
- Calculer l’ETM;
- Tenir compte du degré de certitude souhaité (68 %, 95 %, ou 99 %);
- Calculer les bornes de l’IC.
Voici la même démarche, exprimée par les formules associées à chaque étape.
Un exemple de calcul supplémentaire est présenté ici.
Exemple de calcul de l’IC :
Dans l’exemple présenté à la section sur l’erreur-type de mesure, nous avons établi que l’ETM du test d’habiletés cognitives Wonderlic est de 2,46. Si une personne a obtenu un score de 25, à l’intérieur de quel intervalle de confiance est-il probable à 95 % que se trouve le score vrai (donc le véritable niveau d’habileté cognitive) de la personne? Le calcul de l’IC se fait ainsi :
Interprétation : il y a 95 % de probabilité que le score vrai de cette personne au Wonderlic se situe entre 20,18 et 29,82. On pourra aussi dire que la marge d’erreur à 95 % du Wonderlic est de plus ou moins 4,82 points.
Limite de l’intervalle de confiance :
Le degré de certitude que le score vrai de la personne évaluée se situe à l’intérieur de l’intervalle de confiance n’est jamais de 100 %, même s’il peut toutefois s’en rapprocher fortement (95 %, 99 % ou même plus). Or, plus le seuil de probabilité est élevé, plus l’IC est grand et l’interprétation du score perd alors de sa pertinence. Il s’agit donc de trouver un équilibre raisonnable entre le degré de certitude recherché et la précision de l’IC. C’est pourquoi de nombreux psychométriciens recommandent d’utiliser un seuil de 90 % ou de 95 % pour le calcul de l’intervalle de confiance.