La transformation d’un score brut en score Z (ou score standard) est simplement l’équivalent de sa distance à la moyenne exprimée en écart-type. Lorsqu’une échelle de mesure d’un score est transformée en score Z, la moyenne est toujours de 0 et l’écart type est toujours égal à 1. De plus, lorsque le score brut est au-dessus de la moyenne, le score Z est positif et négatif lorsque le score brut est sous la moyenne. Ceci devient évident lorsqu’on examine la formule du score Z. En effet, si le score brut à transformer (x_i) est égal à la moyenne (X), même en divisant par l’écart-type (s), le résultat est égal à 0. Ceci veut donc dire qu’en score Z, la moyenne de la distribution normative devient 0 et que l’étalonnage de la distribution (l’écart-type) est de 1,00 et s’étend généralement de -3,00 à 3,00. Toujours en examinant la formule, on remarque que si le score brut (x_i) se situe sous la moyenne (X), le score Z sera effectivement négatif et inversement. Il est également essentiel de tenir compte des décimales lors du calcul afin de positionner un score dans la distribution avec une étendue aussi restreinte. 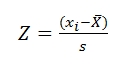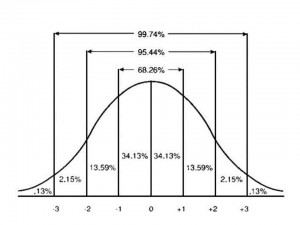Voici la formule pour transformer un score brut en score Z.Dans une distribution (approximativement) normale, la transformation en score Z permet, d’une part, de positionner par rapport à la moyenne de la distribution et, d’autre part, de calculer avec précision le pourcentage des observations contenues entre n’importe quelles valeurs Z. La figure présente ces pourcentages pour des valeurs Z spécifiques de la distribution. On remarque qu’entre la moyenne et un score se situant à un écart-type (ou -1 écart-type car la courbe est symétrique) on trouve 34,13% de toutes les observations de l’échantillon. Cette propriété de la courbe normale est très utilisée en statistique et en psychométrie, notamment pour calculer les intervalles de confiance des scores vrais.