L’erreur-type de la différence, notée ETMdiff, permet de déterminer, selon un seuil de probabilité donné, si la différence entre deux scores observés est attribuable à une réelle différence entre les scores vrais ou s’il s’agit d’une variation normale compte tenu de l’erreur de mesure. L’ETMdiff sert à la comparaison des scores de deux personnes à un même instrument psychométrique, ou à la comparaison des scores d’une même personne à deux passations différentes d’un même instrument. Par exemple, l’ETMdiff est utile pour étudier les changements de scores observés suite à une intervention (pré-test / post-test). En effet, au regard de l’erreur de mesure de l’instrument, il est parfois souhaitable d’éviter d’accorder trop d’importance à des petits écarts. Il faut néanmoins être en mesure d’estimer la probabilité que la différence entre les scores observés soit due à une différence réelle entre les scores vrais (par exemple, entre les aptitudes de deux personnes). En tenant compte de l’étendue possible dans laquelle chacun des scores peut fluctuer (ETM), il est possible qu’un écart entre deux scores ne soit pas suffisamment significatif pour affirmer qu’il existe une réelle différence entre les scores vrais.
Le calcul de l’ETMdiff permet donc de déterminer un seuil au-delà duquel on peut objectivement considérer que la différence entre les scores est suffisamment grande pour affirmer qu’elle n’est pas due seulement à l’imprécision de l’instrument utilisé (c’est-à-dire à l’erreur de mesure).
En raison de l’influence des erreurs aléatoires des deux scores, l’ETMdiff est toujours plus grande que l’ETM de chacun des deux outils, tel qu’en témoigne le calcul suivant. De plus, comme pour l’ETM et l’IC, l’ETMdiff doit être calculée en fonction du degré de certitude souhaité (68 %, 95 %, ou 99 %). Le calcul de l’erreur-type de la différence est le suivant :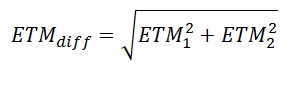 
Si la différence entre les scores observée est plus grande que l’ETMdiff (ajustée selon le seuil de probabilité choisi), alors on peut affirmer, selon le degré de certitude choisi, que cette différence reflète une différence réelle entre les scores vrais, au-delà des variations possibles dues à l’erreur de mesure de l’instrument.
Les exemples suivants illustrent le calcul et l’interprétation de l’erreur-type de la différence.