Le score T est utilisé en suivant la même logique que le score Z, mais un ajustement rend la distribution plus pratique à utiliser (ce qui explique pourquoi il est très souvent utilisé en psychométrie). En effet, par rapport au score Z, il a l’avantage de ne jamais donner de valeur négative et d’avoir une plus grande étendue sans recourir aux décimales. Le score T est en fait le score Z multiplié par 10, auquel on ajoute 50. Ainsi, lorsqu’elle est transformée en score T, la moyenne d’une distribution normale prend la valeur de 50, alors que l’écart-type a une valeur de 10. La valeur de T se calcule donc à partir de la valeur Z préalablement calculée. Voici un exemple de calcul de score T avec un score Z égal à -1,84.

Le calcul montre que l’équivalent d’un score Z de -1,84 est un score T égal à 32. La valeur est arrondie car les scores T sont toujours exprimés par un entier. De même, un score T de 60 correspond donc à un score Z de +1,00, alors qu’un score T de 45 correspond à un score Z de -0,50. On constate que cette transformation élimine effectivement, d’une part, les valeurs négatives que peuvent prendre les scores Z sous la moyenne et, d’autre part, le recours obligatoire aux décimales. Le score T peut donc être une alternative intéressante pour interpréter les résultats de certains tests.

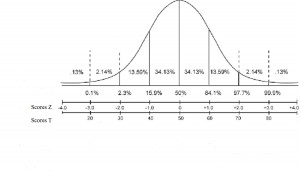
Comme pour le score Z, le score T maintient le lien numérique avec le score brut, c’est-à-dire que la forme d’origine de la distribution est conservée et que l’intervalle entre les unités T est équidistante pour toute l’échelle (voir la figure suivante). Autrement dit, la distance (en score brut) entre les scores T de 50 et 51 est la même qu’entre les scores T de 60 et 61. Cette propriété d’équidistance n’existe pas dans le cas de la transformation en rang (centile, quartile, décile, stanine). La transformation en rang fait l’objet de la section suivante.