Tel que mentionné dans la section sur les Normes, les résultats obtenus à un test psychométrique qui produit un score (ex. : entre 0 et 100) sont généralement interprétés en les comparant à ceux d’un groupe d’individus ayant des caractéristiques similaires, c’est-à-dire à un échantillon appelé normatif. Mais comment comparer un score à l’ensemble de tous les scores d’un échantillon normatif? Il existe deux façons pour exprimer la position d’un score dans une distribution de scores d’un échantillon normatif. La première est de mettre en rang tous les scores, du plus faible au plus élevé, et d’observer à quel rang se situe le score individuel dans cette distribution. Ce type de positionnement en rang s’exprime par quelques transformations du score tel notamment le rang centile, les déciles, les quartiles, les stanines et les stens. L’autre méthode consiste à calculer la position du score individuel (sa distance) par rapport à la moyenne de l’échantillon normatif. Ce type de positionnement axé sur la moyenne s’exprime par des transformations appelées score Z et score T. Notons que dans l’interprétation normative d’un score, les deux méthodes peuvent être employées. Comme les échelles de mesure des construits varient d’un outil à l’autre, la transformation des scores bruts en scores pondérés est une opération qui permet d’exprimer le rang d’un score ou sa position par rapport à la moyenne de manière standardisée.

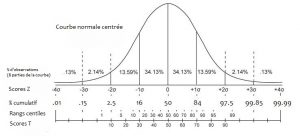
En outre de leur modalité différente d’expression de la position du score, les deux types de transformation se distinguent en termes d’équidistance des unités dans la distribution. Pour la transformation par rapport à la moyenne (score Z et T), la distance entre chaque unité est la même sur toute la distribution tandis que la transformation en rang impose une distorsion de la distance entre les unités, notamment aux extrémités de la distribution. La figure suivante montre bien qu’il y a effectivement davantage de distance entre les premiers et derniers rangs centile qu’entre ceux près de la médiane.

En résumé, la transformation des scores bruts permet donc de positionner le score d’un individu par rapport aux scores des autres personnes de la population à laquelle le client appartient (donc par rapport à la norme). On peut positionner le score en le transformant en rang ou en le transformant en termes de distance par rapport à la moyenne de l’échantillon normatif. Enfin, la transformation d’un score brut permet aussi de se détacher de l’unité de mesure d’origine et d’exprimer le score de manière standardisée. Ceci simplifie énormément l’analyse et l’interprétation des résultats.